Below is a live demo of a software-based ray tracer based as outlined in Computer Graphics from Scratch (chapter 1).  Thus far, the ray tracer has a camera fixed at the origin, and it only determines color by testing for intersection with spheres.  Lighting, shadow, reflections, and other effects have not yet been implemented. Included are controls for adjusting the viewport's dimensions and distance from the origin.  The demo has been slowed down to animate the rendering process, but this can be disabled so that it runs in real-time.  This version of the demo can be downloaded from GitHub.

The basics 

In this article, I will focus primarily on the implementation details of this demo. However, I will briefly outline the ray tracing process implemented thus far.

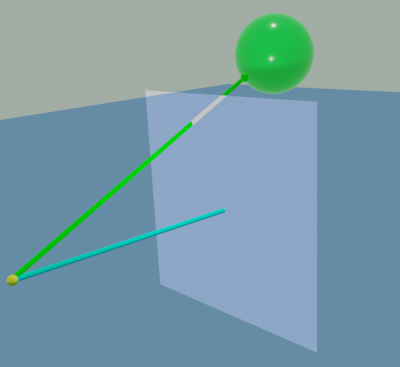
Ray tracing allows us to render a three-dimensional scene onto a two-dimensional screen, which is referred to as the canvas. The process works in the opposite manner of a traditional camera.  Cameras work by taking rays of light that bounce off of objects and focusing them through a lens onto a two-dimensional medium such as film or a digital sensor.  A ray tracer's "camera," which is shown in the accompanying diagram, performs this process in reverse. It sends rays into the scene, and if a ray hits an object, it reports back the color of the object closest to the camera.

 The camera consists of two parts.  The first is a single point within the scene that is referred to as the camera's origin, represented by the yellow sphere. This will serve as the starting point of the rays, and it gives the coordinates of where the camera is situated within the scene. The second component is the camera's viewport, represented by the translucent, white square.  It is a rectangular plane that is centered over the origin but does not contain it, and it behaves like a reverse "film" for our camera. Each pixel on the canvas is mapped onto a point within the viewport, and a ray is cast through this point. If this ray intersects any objects, the corresponding pixel in the canvas is given the closest object's color.

The last detail to work out is how rays are generated. In the reverse of a traditional camera, the process starts with the canvas.  One by one, each pixel of the canvas is mapped to a point on the viewport. This point when combined with the distance between the origin and the viewport creates a direction vector, an arrow that denotes the direction in which the ray will be projected. This vector is then placed at the camera's origin creating the ray, represented by the green arrow. By iterating through each pixel on the canvas in this manner, the renderer can create a two-dimensional representation of a three-dimensional scene.   

 

Implementation Details

As stated above, the current ray tracer implementation is based on the implementation from the first chapter of Computer Graphics from Scratch. It currently only renders the colors of the objects within the scene without consideration for lighting, shadows, and reflections. Spheres are the only type of object implemented. The camera itself is fixed. Its origin is situated at the global origin, or three-dimensional center, of the scene, and the viewport is perpendicular to the global z-axis, the line along which coordinates of depth are measured.  In short, it cannot be moved or rotated.

One area in which I have decided to diverge from the book's implementation is in the structuring of the code.  This is done primarily to facilitate the addition of other types of objects beyond spheres to the scene. The book's pseudocode uses structs to organize the data of objects within the scene, and the core functionality of the renderer is divided into discrete functions. Most importantly, this includes the code to test the intersection between rays and spheres.  

The difficulty arises when adding other types of shapes.  Each type of shape requires its own method to test for ray intersections.  Under the book's implementation, the renderer's code would have to determine the type of shape being tested at runtime and select the appropriate test, and this in turn would require the render's code to be modified each time a new type of shape was added. By utilizing an object-oriented design, each type of shape is now responsible for providing the appropriate test instead of the renderer.  As such, new types of shapes can be passed to the renderer without ever touching the renderer's code. 

For the sake of experimentation, I have also added sliders that will change the viewport's dimensions and its distance from the origin.  Adjusting these parameters and rendering demonstrates a few interesting characteristics of the rendering process.  First, if the height or width is increased, this will have the effect of shrinking the rendered objects on the canvas in the affected axis.  Similarly, decreasing these variables will scale up the objects in the affected dimension.  This behavior makes sense, as shrinking the viewport will make the objects appear larger in comparison.  Another interesting effect can be observed by making the height and width negative.  This flips the image in the affected dimension.  This occurs because the canvas' pixels are mapped to the opposite side of the viewport. 

Altering the distance between the origin and the viewport has similar results.  As the distance is reduced towards zero, the objects again appear to become smaller.  This occurs because the angles between the generated rays increase, thus increasing the field of view and rendering a larger portion of the scene.  Similarly, increasing the distance decreases the angle between the rays and renders a smaller portion of the scene, which in turn increases the size of the objects relative to the viewport. However, if the distance between the viewport and the camera's origin is expanded beyond the location of the objects in the scene, then those objects will be behind the viewport and thus will no longer be rendered.

Potential Enhancements

At this juncture, my current plan is to first implement the book's features, and then look into other features to add.  I can, however, speculate about the improvement of the features that have been built thus far. 

One major feature that this current implementation is lacking is the ability to change the camera's orientation.  Fortunately, this option should be relatively simple to implement.  Recall the process by which the ray is created. First, the direction that the ray will be cast is generated in the coordinate space of the camera. As such, changing the orientation of the camera relative to the scene should only require rotating each of the generated direction vectors by a single rotation matrix representing the orientation of the camera.  Similarly, moving the camera should only require translating the origin point. 

Another area for improvement is to optimize the test for ray intersections with objects. Currently, each ray is tested against each object resulting in m X n number of tests, where m is the total number of pixels in the canvas and n is the number of objects.  Using data structures to partition the space, such as an octree, should pare down the number of objects being tested, and thus improve performance.