The Basics 

In the real world, light is the form of energy that allows us to see and capture images. Individual packets of light called photons strike the surface of objects.  This light will interact with the surface in various ways: some will be absorbed, some will be reflected, and some will be scattered throughout before being reflected away.  How the light interacts with the object's surface is determined by the materials it is composed of, and these interactions determine what characteristics the light will take on. In turn, the alterations of light determine what type of image we will see.  The ray tracer uses its implementation of lights to simulate light sources, and it uses algorithms called shaders to simulate how the light interacts with the materials. 

Color

Before we can discuss how light works in the computer, we must take a brief detour to discuss color.  Each portion of our image is represented by a dot called a pixel.  Each pixel, in turn, is composed of three colored lights: one red, one green, and one blue, which are referred to as color channels.    Varying the intensity of how brightly lit each channel is, we can create different colors. In the color model used by the ray tracer, the intensity of each color is represented by a whole number from 0 to 255, with 0 representing a completely dark channel, and 255 representing a completely lit channel.  With three channels, each having 256 possible values, we can create 16,777,216 possible colors.

 

Lights

Recall from the previous article how the ray tracer works. For each pixel in our output image, the ray tracer sends a ray into the scene and determines which point in the scene corresponds to the pixel in the image, and then it determines the color of the object at that point.  Now, before returning the color, we add an extra step. We go through each light within the scene and determine how it interacts with the object at the point being processed using code called shaders. The shaders calculate what fraction of the light that strikes the surface at this point is reflected toward the camera. Ideally, the total amount of light reflected should be a value between zero and one, scaling each channel by the amount of light.  Each color channel is then multiplied by this fraction, attenuating the respective colors based on the amount of light sent back.  If no light is returned, then the pixel will be black, and if all light is returned, then the color will be returned in full. 

The light model within this ray tracer is concerned with two attributes of light, the amount of energy it emits or its intensity, and the direction the light is coming from.  All light is modeled within the computer as rays. The main difference between each type of light is how it determines the direction that these rays are coming from relative to the surface being processed. In this iteration, three types of lights are being modeled: ambient, point, and directional.  

The first type, ambient lighting, is the simplest to model.  It is simply an intensity value that is automatically applied at each point without further processing. This is done to represent all of the light within the scene that is scattered by the air and various surfaces, and it ensures that no part of the scene is without the influence of light. Because it is scattered, it is presumed by the computer to be coming equally from all directions, and thus, the computer can ignore its direction. As it represents all of the scattered light, there is only one ambient light within a given scene. 

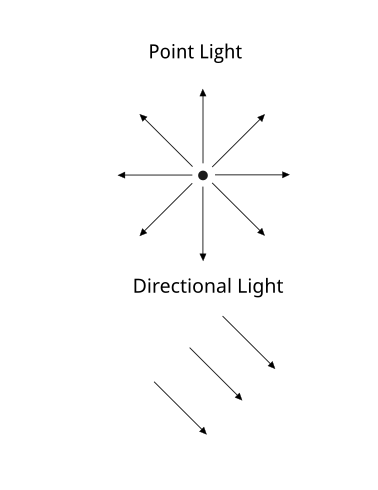
The next type of light, the point light, is the ray tracer's analog to a real-world light bulb. It has an intensity value between zero and one, and it has a point that represents its location within the scene. Light emanates as rays cast equally in all directions from its location.  It provides a method to calculate the direction the light is coming from relative to the surface, which will be important later in calculating the light's interaction.

The last type of light implemented is the directional light.  This light is meant to simulate a light source at a distance, such as the Sun. These light sources are so far away that the angle between light rays is negligible.  As such, all rays coming from the source are effectively parallel.  The directional light thus has two properties, an intensity value, and a directional vector which denotes the direction the light rays are coming from.   

 

Shaders

Now that we have our lights, we need a way to simulate how lights interact with the surfaces of our objects.  This is where shaders come in.  Shaders calculate how much light reaches the surface of the object at the point being evaluated, and they determine how that light is reflected toward the camera.  The effects of these shaders combine to determine the general look of the objects. 

Within this demo, each non-ambient light source is processed by each shader.  The shaders utilize the direction in which each light strikes the object's surface, and they then use this information to determine how much of the energy from each light will be returned to the camera. It should be noted that each shader uses this directional information differently, which will be illustrated below in the discussion of specific shaders. By adding these attenuated intensities together with the ambient light, the tracer can calculate the total amount of light hitting the surface at that point. Each color channel is then multiplied by the intensity to calculate the final output color.

Currently, there are two types of shaders implemented: diffuse and specular.  Both of these shaders take a direction vector representing the direction from which the light is coming and use this to calculate the amount of light sent back to the camera.  Specifically, each shader uses a different vector as a point of reference, and it calculates the cosine of the angle between the light's direction and this reference vector.  The cosine produces values between -1 and 1, which is perfect for producing a fraction by which to attenuate the lights. A value of 1 occurs when the two vectors are perfectly aligned, and the values decrease as the angle increases.  Once the angle between vectors becomes greater than 90 degrees, the cosine becomes negative, which we ignore.

 

The diffuse shader reflects light equally in all directions.  It is generally responsible for the fairly even distribution of lighting over an object's surface. As such, it only takes into account the direction from which the light is inbound to determine how much to reflect toward the camera. It is thus concerned with how much light is being reflected at that point.

To make this calculation, it utilizes the surface's normal which is represented by the vertical black line.  This is a vector that is perpendicular to the surface at the point being analyzed.  It uses the dot product to calculate the cosine of the angle between the normal and the light's direction vector, represented by the blue line.  When the light is directly overhead (and thus aligned with the normal vector), the light is spread over the least amount of surface area, and thus all of it is reflected.  As the angle between the light and normal increases, the light is spread over a larger area, and thus less light is reflected by any given point. Notice how in the demonstration above, the reflected light, represented by the thick horizontal line, goes from yellow to black as the light moves away from the normal.  Less light is reflected and thus the yellow becomes darker and moves toward black. 

Our other shader, the specular shader, creates highlights for the object. Unlike the diffuse shader, the specular shader assumes that light is not reflected equally in all directions.  Instead, the shinier the object is, the more concentrated the area over which the light will be reflected is. Thus, shinier objects will reflect light over a narrower area than dull objects, resulting in them having more concentrated highlights.  

The specular shader must determine how much of that light is reflected toward the camera. It does so by first calculating the direction in which the incoming light, represented by the blue line, is reflected off of the object represented by the purple line. It does this by calculating the angle between the normal, represented by the vertical black line, and then it reflects the light on the opposite side of the normal by the same angle. It then calculates the cosine of the angle between the reflected light and vector from the point being analyzed to the camera, represented by the green line. Notice again how as the angle between the reflected light and the camera increases, the reflected color again becomes darker. 

Finally, to allow for different levels of shininess among objects, the shader raises the result to an exponent. Because cosine values are always 1 or less, raising the returned value to some exponent will create even smaller numbers, with larger exponents attenuating the light much more sharply than those with smaller exponents. Thus, larger exponent values will dim the object more but make it appear much shinier than objects with lower exponent values.  In the above demo, the green sphere has a shininess exponent of 10, whereas the blue and red spheres have shininess exponents of 500.

Implementation Details

Once again, I have continued to utilize an object-oriented architecture.  The lights are implemented as separate classes. Originally, I intended to make all lights share a common interface. However, as each light is processed differently, the lights were not good candidates and required separate handling.  Each light does have an intensity.  Additionally, the directional light implements a direction attribute which returns its direction vector, and the point light implements a position attribute and a getDirection method, which calculates a direction vector from a point to the light source. 

Another significant point of departure from the book's implementation involved the creation of distinct shaders. Within the book, the shader code is part of the lighting calculating function. I have separated this code into its own classes, and instances have been attached to the respective objects which they will shade.  This will allow for different objects to use different types of shaders, which in turn will alter their appearance.  Currently, each sphere has an instance of both the diffuse shader and the specular shader, which are attached under those properties.  Each shader instance also maintains its settings as its attributes, separating them from the parent objects.  

One final change is the location of the code for calculating the lighting itself.  Lighting calculations for the point and directional lights are currently delegated to the shaders themselves.  This is handled within methods within the common base class of both shaders. This was done in case future shader implementations treat light calculations in different ways. 

 

Potential Enhancements

One of the biggest potential enhancements would be to make new types of shaders. There are a variety of different types of shaders, many based on more physically realistic models. This could allow for more realistic and detailed models. To accommodate this, the objects would instead maintain a list of shaders instead of the two separate instances currently maintained.  

Another possible enhancement would be to include shaders that model refraction instead of reflection. Refraction models the bending of light through transparent and translucent materials, and thus transparent materials such as glass and water could be modeled.  

The lighting model itself is also quite limited.  It currently does not account for attenuation at distance, and it is only white light. Colors can be implemented as an intensity value through each color channel instead of a single intensity. Each color channel would then be multiplied by its respective intensity instead of multiplying each channel by a single intensity.  

Distance attenuation will be a bit more complicated.  Physically, light falls off according to the inverse square law, which states that the amount of light reaching a specific area decreases proportionally to the square of the distance to which it is traveling.  I did experiment with this briefly during this implementation.  However, there is a slight difficulty in calibrating the intensity and the distance.  To properly light the scene, the current light model requires an intensity no greater than one.  Applying distance to the intensity rapidly attenuates it.  I will have to research and experiment further to find a workable balance between the effects.